Ediz Ferit Kula

Ediz Ferit Kula

MSc Student in Computational Science at Imperial College London.

Parallel Programming Projects

The two projects where I used parallel programming during my master’s at Imperial are summarised:

  1. Parallelising PDE Solver
  2. Optimising Mineral Separation Circuits

1. Parallelising PDE Solver

Reaction-diffusion equations:

\[\frac{\partial C_1}{\partial t} = (C_1 (1 - C_1) - f C_2\frac{C_1 - q}{C_1 + q})/\epsilon + D_1 \nabla^2 C_1\] \[\frac{\partial C_2}{\partial t} = C_1 - C_2 + D_1 \nabla^2 C_1\]

Domain is discretised using a Forward Time Centered Space (FTCS) scheme.

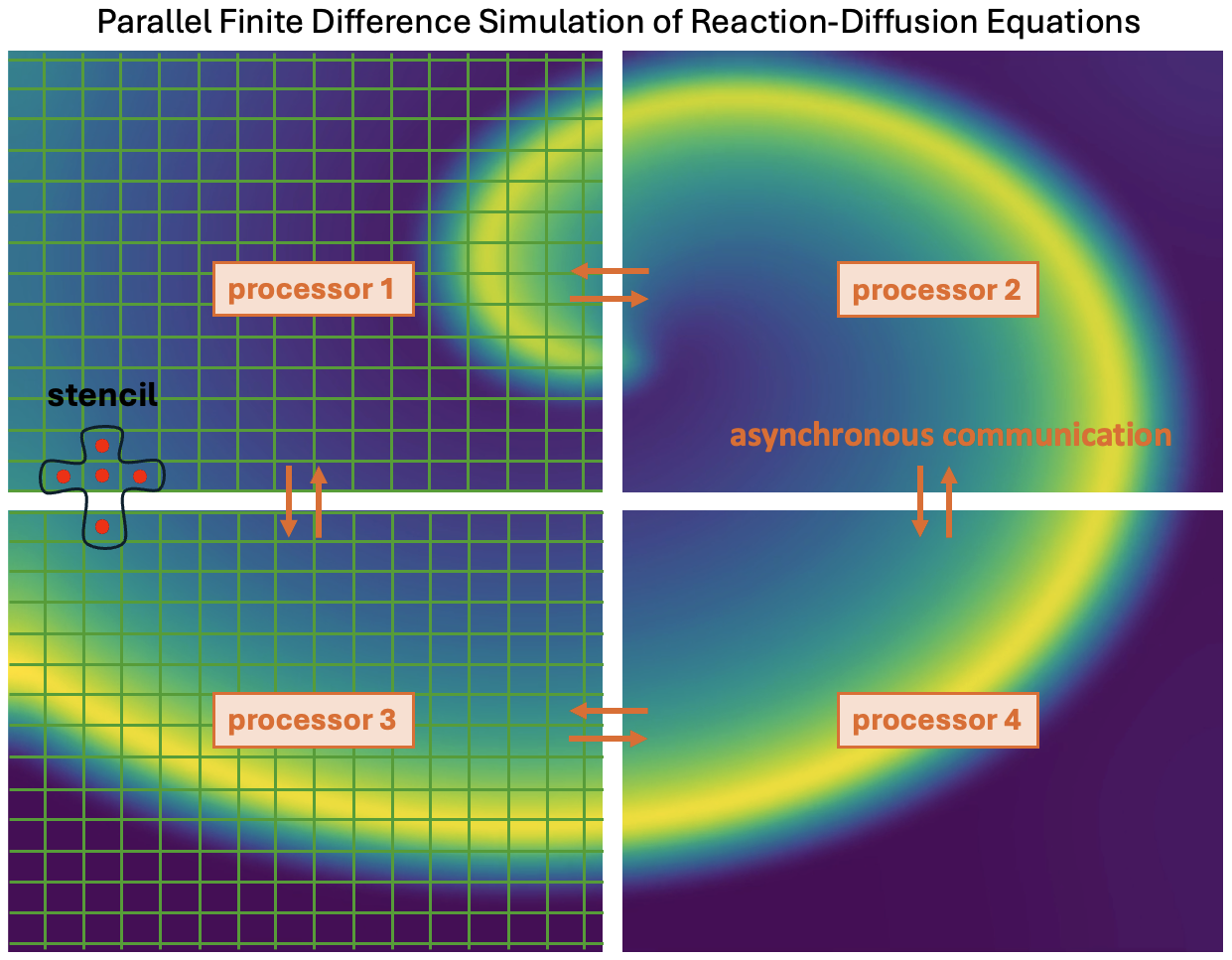
Speedup vs Clusters


Simulation is divided into rectangular domains that are as close to square as possible to reduce communication amount. Communications are set up using MPI in the form of non-blocking peer-to-peer communication, with each process communicating only with its vertical and horizontal neighbours.

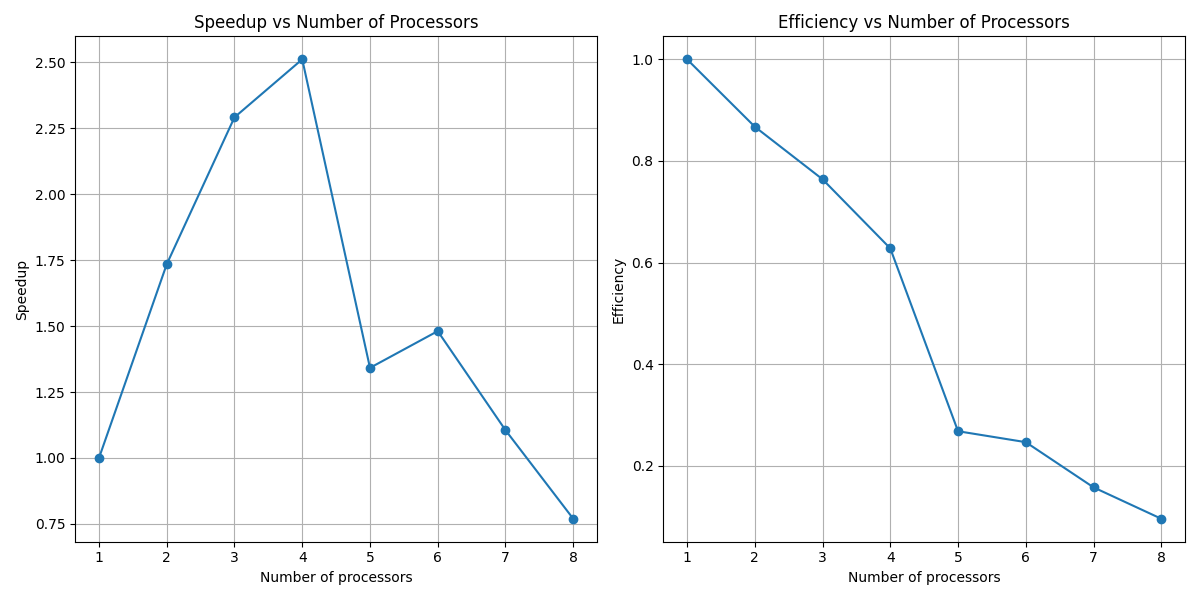
Speedup vs Clusters


I tested the performance using a number of cores and plotted the speedup and efficiency results, as seen above. With 4 processors, we can gain 2.5 times speedup.

Simulation video with periodic boundary conditions:

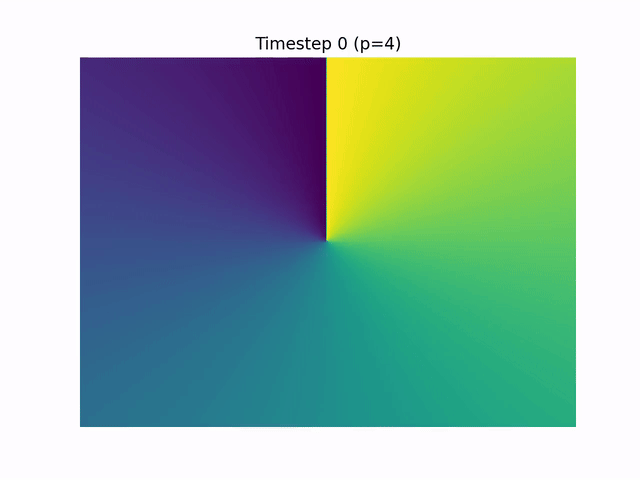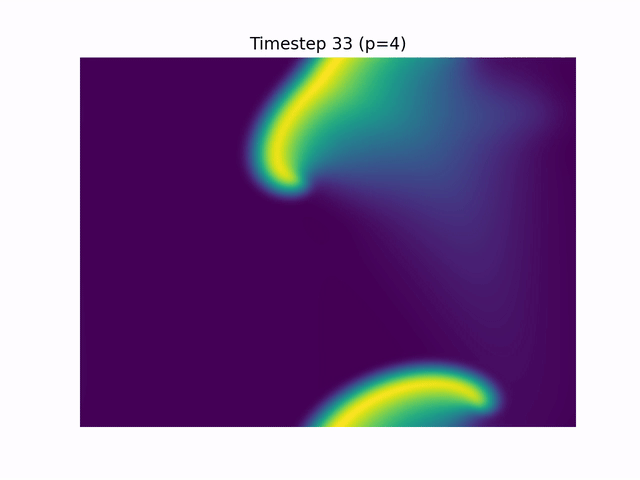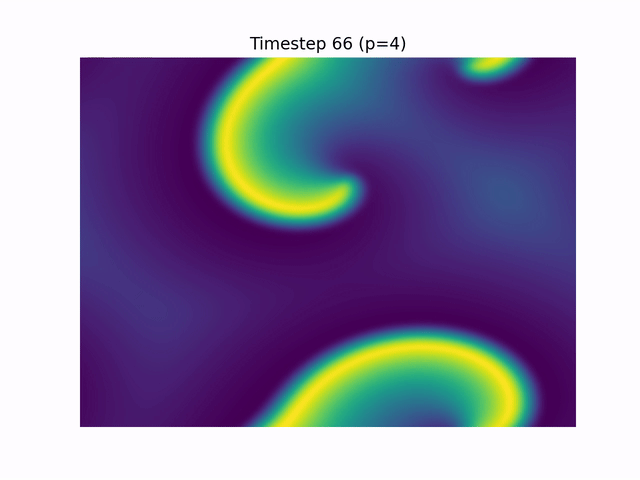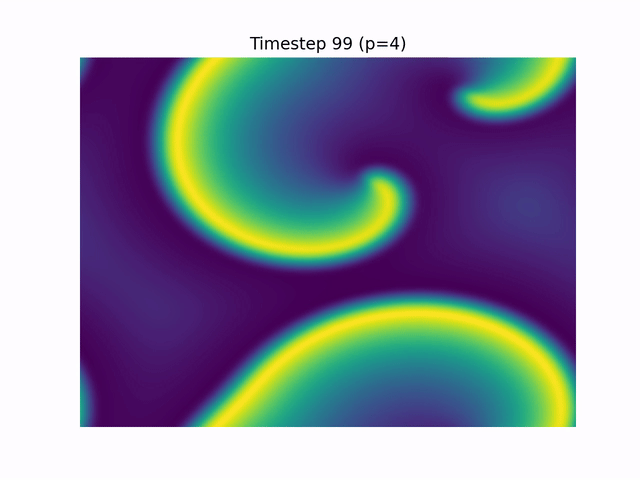
Speedup vs Clusters


2. Optimising Mineral Separation Circuits

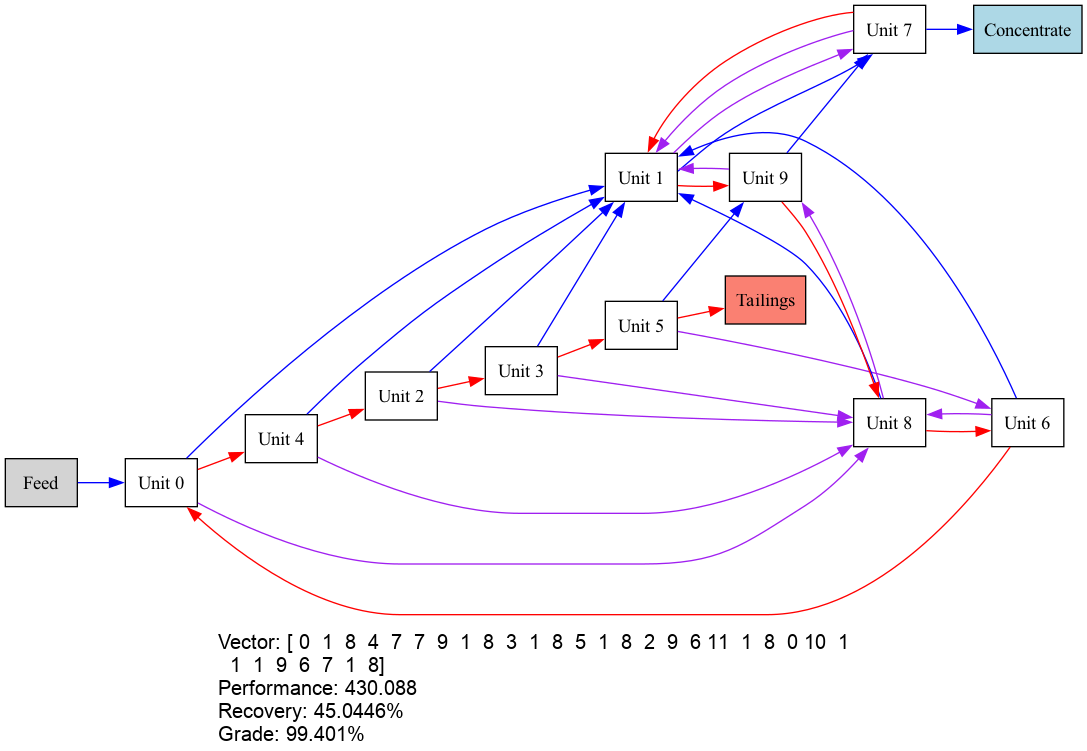
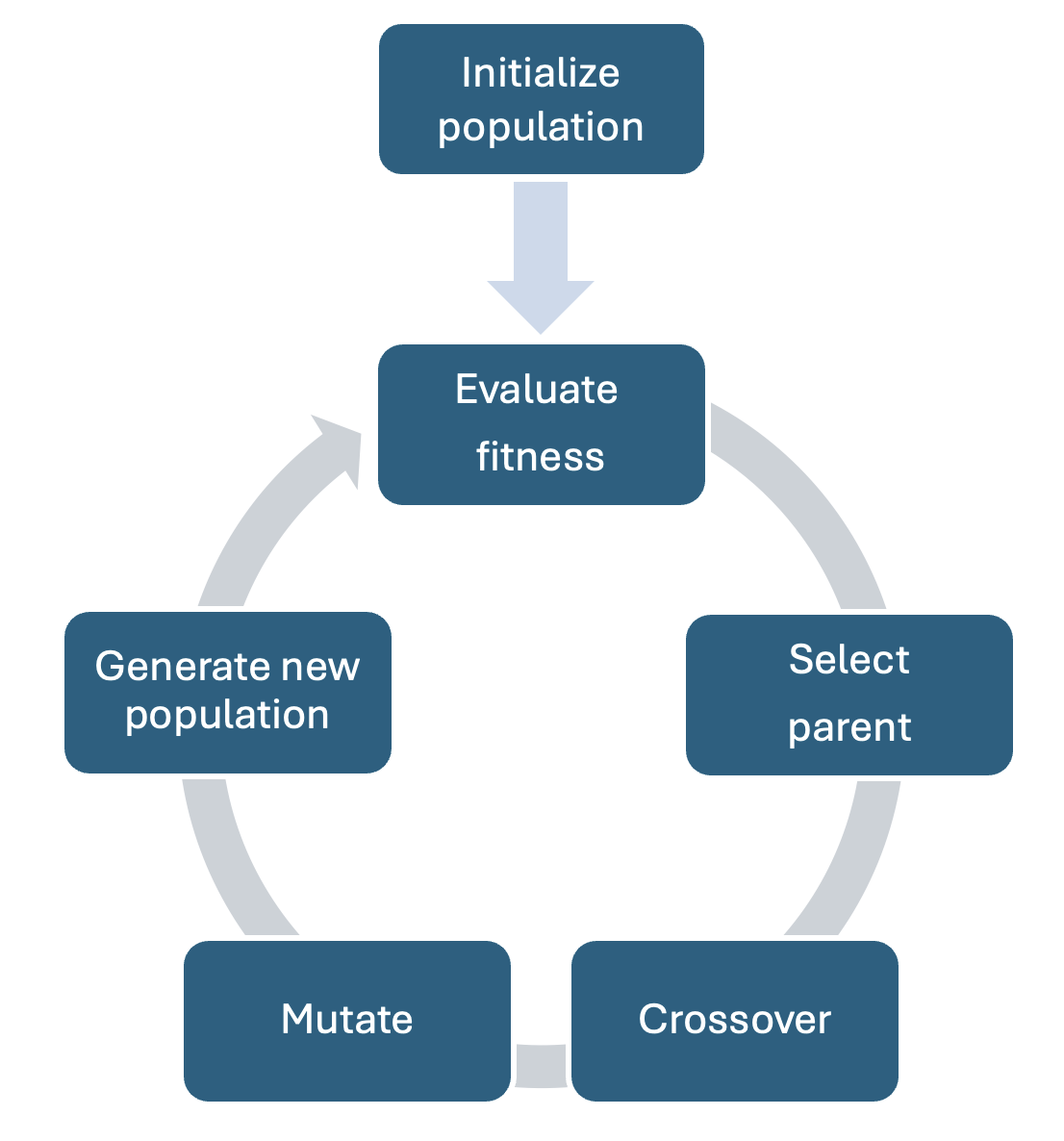
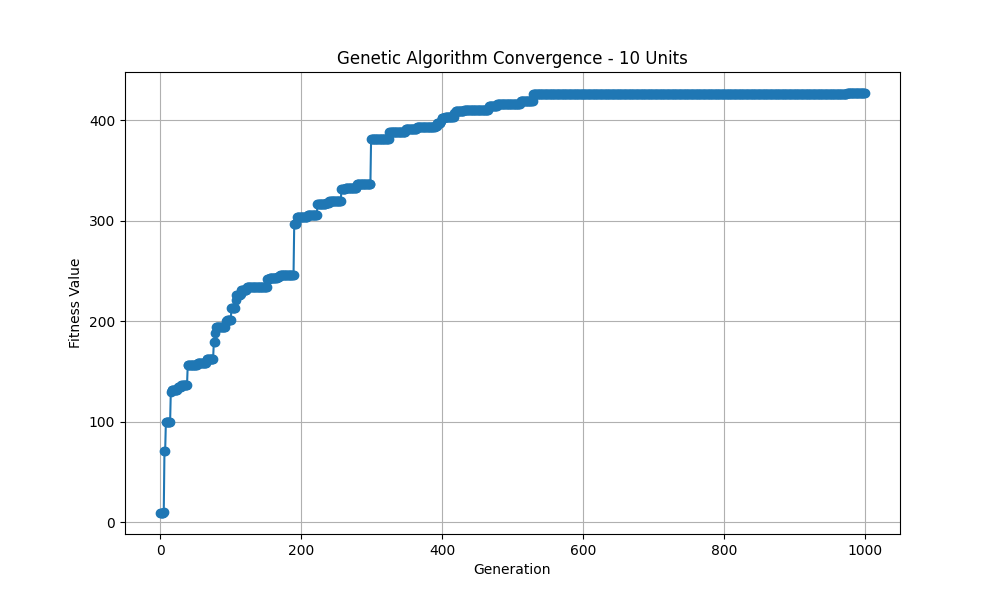
This project was a group project included in my master’s program at Imperial College London. Here, I implemented a genetic algorithm to find the optimum circuit configuration to separate minerals with the maximum performance.

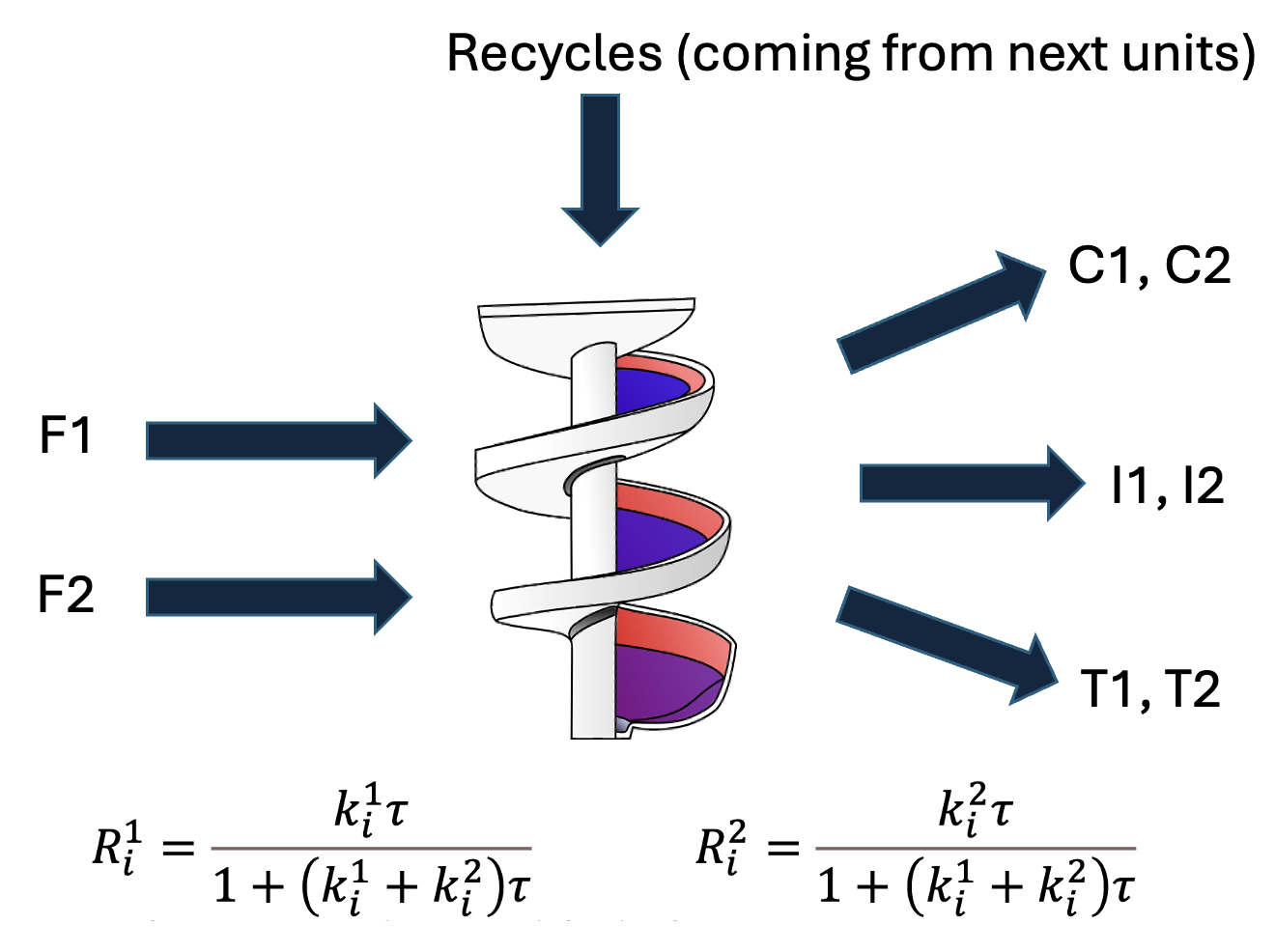
Real circuit Circuit flow

Optimum Circuit Configuration

Best Circuit
The above circuit is the one giving the maximum performance in separating a valuable mineral called 'Gerardium' (not a real mineral). It will extract the maximum amount of Gerardium while maintaining high purity.

Genetic Algorithm

Genetic Algorithm Workflow
I implemented a genetic algorithm to find the best circuit. It includes two main phases: exploration and exploitation. Random crossovers and mutations are used.

Convergence

Genetic Algorithm Convergence
Genetic algorithm converges after 500 generations, as shown in the figure above. The larger jumps in the plot represent the mutations, while smaller but consistent improvements represent the exploitation.

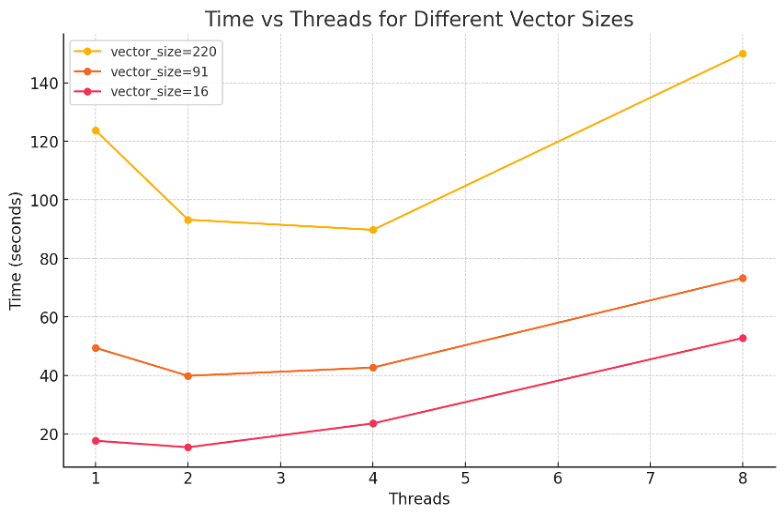
Parallelisation with OpenMP

Time vs Threads


The genetic algorithms are easily parallelisable. I tested the algorithm by parallelising it with OpenMP, which is straightforward to implement but limited by the number of cores on a single computer. In contrast, MPI allows for scaling across multiple processors on different computers, offering virtually unlimited computational power. However, MPI is more complex to implement due to the need for managing communication between processors.

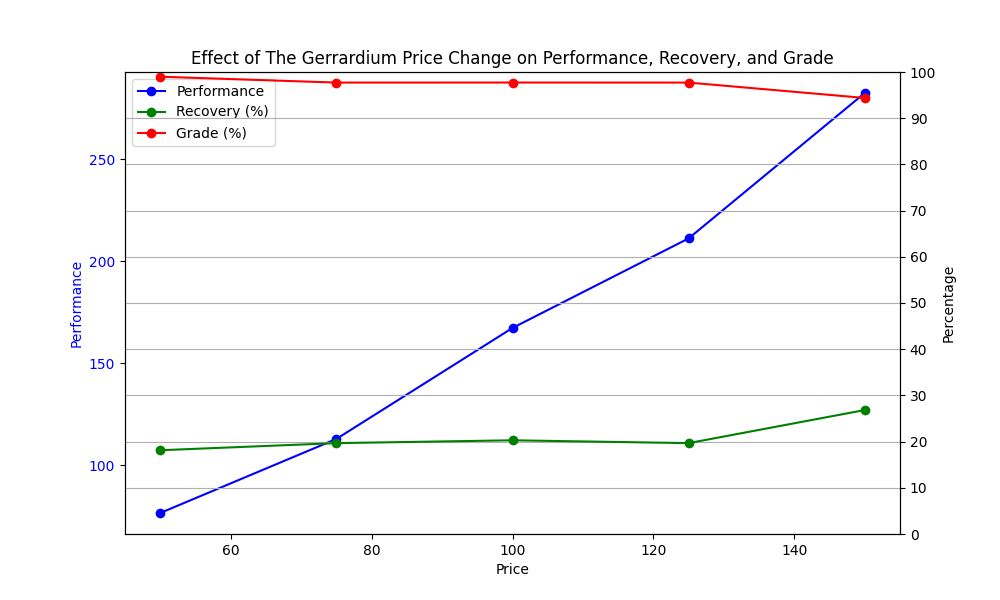
How Does the Optimum Cirucit Change with the Varying Values of Geraridum

Economic Effect of Gerardium Price Change
Lastly, in the above figure, we see that if Gerardium price increases, the purity of the concetenate decreases slightly as seen in the red line. This balance depend on the cost of waste in the concatenate and amount of Gerardium extracted.